Электрическое поле, характеристики – напряженность, потенциал

Лекция № 13 Электрическое поле. Напряженность. Потенциал. Разность потенциалов. Напряжение.

Электрическое поле, напряженность.

1.Напряжённость электрического поля

Основной закон электростатики — закон Кулона — позволяет вычислить силу взаимодействия двух точечных зарядов. Данный закон, однако, ничего не говорит нам о том, каким образом осуществляется это взаимодействие. Как так получается, что один заряд может действовать на другой даже на весьма большом расстоянии?

1.1 Электрическое поле

Физическим объектом, передающим взаимодействие между зарядами даже сквозь пустоту, оказалось электромагнитное поле. Решающими здесь оказались идеи и труды двух великих учёных XIX столетия — Фарадея и Максвелла. Экспериментальным подтверждением теории близкодействия явилось открытие электромагнитных волн.

Неподвижные заряды не создают магнитного поля; поэтому, пока мы изучаем электростатику, мы будем говорить только об электрическом поле. Итак: Электрический заряд создаёт вокруг себя электрическое поле, которое, в свою очередь, действует с некоторой силой на другие заряды.

Электрическое поле не нуждается в какой-то специальной среде, которая являлась бы его носителем. Оно может возникать как в веществе, так и в вакууме, и является, наряду с веществом, альтернативной формой существования материи.

По современным физическим представлениям электрическое поле является первичным физическим объектом: мы пока не можем сказать, каково его внутреннее устройство (точно так же мы не можем сказать, например, из чего состоит электрон). Мы можем лишь изучать свойства электрического поля, устанавливать законы его поведения и использовать эти законы в своих целях.

Источниками электрического поля являются электрические заряды. Индикатором для обнаружения поля также является электрический заряд — так называемый пробный заряд. По действию на пробный заряд мы и можем судить о наличии электрического поля в данной области пространства. Кроме того, с помощью пробного заряда мы можем исследовать величину поля в различных пространственных точках. Разумеется, для этого пробный заряд должен быть точечным.

Опыт показывает, что сила, с которой поле действует на пробный заряд, прямо пропорциональна величине заряда. Поэтому отношение силы к заряду уже не зависит от величины заряда и является характеристикой поля.

Напряжённость электрического поля — это отношение вектора силы F , с которой поле действует на пробный заряд q, к самому пробному заряду (с учётом его знака):

E = F/ q                                     (1)

Напряжённость поля, как видим, является векторной величиной. В каждой точке пространства электрическое поле характеризуется вектором напряжённости. Поле считается заданным, если нам известна зависимость вектора напряжённости от координат точки и, вообще говоря, от времени.

Как следует из определения, напряжённость измеряется в Н/Кл. Общепринятая единица напряжённости есть В/м. Мы скоро увидим, что это одно и то же.

Если напряжённость поля известна, то формула (1) позволяет найти силу, которая действует на точечный заряд со стороны электрического поля:

F = qE

Сила и напряжённость, таким образом, являются коллинеарными векторами. Если заряд положительный, то сила направлена в ту же сторону, что и напряжённость. Если заряд отрицательный, то сила направлена противоположно напряжённости. Одна из основных задач электростатики – нахождение напряжённости поля, создаваемого данной системой зарядов. Рассмотрим некоторые примеры.

 1.2 Напряжённость поля точечного заряда

Определение модуля и направления вектора напряжённости поля точечного заряда — это самая простая и легко решаемая задача. Рассмотрим положительный точечный заряд q, находящийся в вакууме. Поместим на расстоянии r от него положительный пробный заряд q₀. Со стороны заряда q на пробный заряд действует сила отталкивания, поэтому напряжённость поля положительного заряда q направлена от него (рис. 1):

Рис. 1 Напряжённость поля положительного заряда

Величина силы отталкивания равна:

F = kqq₀/ r ²

Делим силу на пробный заряд q₀ и находим модуль напряжённости поля заряда q:

E = kq/r²     (2)

Пусть теперь заряд, создающий поле, будет отрицательным; модуль этого заряда также обозначаем q. Сила, действующая на положительный пробный заряд, станет силой притяжения. Поэтому напряжённость поля отрицательного заряда направлена к нему (рис. 2):

Рис. 2 Напряжённость поля отрицательного заряда

 

Модуль напряжённости поля снова находится по формуле (2). Если заряд q находится в среде с диэлектрической проницаемостью ε, то сила его действия на пробный заряд уменьшается в ε раз:

F = kqq₀/εr²

Следовательно, в ε раз уменьшается и напряжённость поля:

E = kq/εr²                (3)

Модуль напряжённости поля точечного заряда q находится по формуле (2) в вакууме и по формуле (3) в диэлектрической среде. Вектор напряжённости в данной точке направлен вдоль прямой, соединяющей точку с зарядом: от заряда при q > 0 и к заряду при q < 0.

По мере удаления от заряда модуль напряжённости поля убывает пропорционально квадрату расстояния от точки наблюдения до заряда. На рис.3 дано примерное графическое представление электрического поля точечного заряда в пространстве (показаны векторы напряжённости поля в различных точках).

Рис. 3 Векторы напряжённости поля точечного заряда.

Ниже мы познакомимся с более удобным способом изображения поля — линиями напряжённости.

1.3 Поле равномерно заряженной плоскости

Важным примером системы зарядов является заряженная плоскость. В качестве бесконечной плоскости мы можем рассматривать любую плоскую пластину, если расстояние от точки, в которой ищется поле, до пластины много меньше размеров самой пластины.

Заряженная плоскость характеризуется величиной поверхностной плотности заряда. Что это такое? Возьмём небольшой участок плоскости площадью S. Пусть заряд этого участка равен q. Тогда поверхностная плотность заряда определяется как отношение заряда к площади:

σ = q/S .

Иными словами, поверхностная плотность заряда — это заряд единицы площади.

Поверхностная плотность заряда может меняться от участка к участку. Но если на любом участке плоскости поверхностная плотность заряда одинакова (σ = const, т. е. заряд распределён равномерно), то плоскость называется равномерно заряженной.

Вектор напряжённости поля равномерно заряженной плоскости перпендикулярен плоскости; он направлен от плоскости, если плоскость заряжена положительно, и к плоскости, если плоскость заряжена отрицательно (рис. 12).

Рис. 4 Поле равномерно заряженной плоскости

Самое удивительное заключается в том, что величина напряжённости поля не зависит от расстояния до плоскости. Она оказывается равна:

E = σ /2ε₀                 (4)

Эта формула справедлива для вакуума (мы принимаем её без доказательства). В среде с диэлектрической проницаемостью ε поле, как обычно, уменьшается в ε раз:

E = σ/2ε₀ε               (5)

Пример заряженной плоскости важен потому, что мы встречаемся здесь с понятием однородного поля. Электрическое поле в данной области пространства называется однородным, если вектор напряжённости поля одинаков в каждой точке области. Иными словами, напряжённость поля в каждой точке рассматриваемой области имеет одно и то же направление и неизменную величину.

Поле точечного заряда, например, не является однородным. В самом деле, напряжённость поля точечного заряда может меняться от точки к точке как по величине, так и по направлению (она обратно пропорциональна квадрату расстояния до заряда и направлена вдоль прямой, соединяющей заряд с точкой наблюдения).

А вот заряженная плоскость создаёт однородное электрическое поле в каждом из полупространств, на которые она разбивает пространство. Напряжённость этого поля вычисляется по формулам (4) или (5).

1.4 Линии напряжённости электрического поля

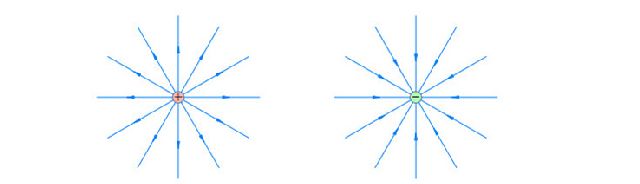
Давайте вернёмся к пространственной картине поля точечного заряда. Вместо векторов напряжённости в разных точках нарисуем более приятные глазу линии напряжённости (рис. 5):

Рис. 5 Линии напряжённости поля точечного заряда

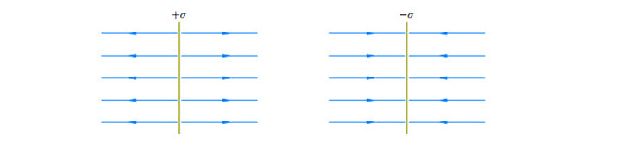
Линии напряжённости идут вдоль векторов напряжённости, указывают направление этих векторов и даже содержат информацию об их абсолютных величинах: чем гуще расположены линии напряжённости, тем больше величина напряжённости поля в данной области пространства. Аналогичную картину линий напряжённости мы можем нарисовать и для заряженной плоскости (рис. 6). Как видим, линии напряжённости однородного поля являются участками параллельных прямых.

Рис. 6 Линии напряжённости поля заряженной плоскости

Линии напряжённости можно провести и в произвольном электрическом поле. Каким образом? В каждой точке пространства вектор напряжённости поля направлен по касательной к линии напряжённости. Линии напряжённости как бы «подстраиваются» под векторы напряжённости, «обтекая» их по касательной (рис. 7):

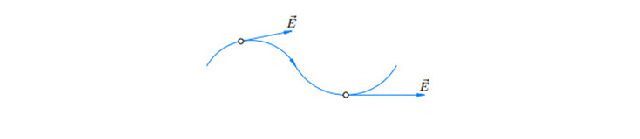Рис. 7 Линия напряжённости Линии напряжённости всегда начинаются на положительных зарядах и заканчиваются на отрицательных.

1.5 Потенциал электрического поля

Потенциальность электростатического поля

Оказывается, что сила, с которой электростатическое поле действует на заряженное тело, также является консервативной. Работа этой силы, совершаемая при перемещении заряда, называется работой электростатического поля. Имеем, таким образом, важнейший факт: Работа электростатического поля не зависит от формы траектории, по которой перемещается заряд, и определяется лишь начальным и конечным положениями заряда. Работа поля по замкнутому пути равна нулю. Этот факт называется также потенциальностью электростатического поля.

Как и поле силы тяжести, электростатическое поле является потенциальным. Работа электростатического поля одинакова для всех путей, по которым заряд может двигаться из одной фиксированной точки пространства в другую. Строгое математическое доказательство потенциальности электростатического поля выходит за рамки школьной программы. Однако «на физическом уровне строгости» мы можем убедиться в справедливости этого факта с помощью следующего простого рассуждения.

Нетрудно видеть, что если бы электростатическое поле не было потенциальным, то можно было бы построить вечный двигатель! В самом деле, тогда существовала бы замкнутая траектория, при перемещении заряда по которой поле совершало бы положительную работу (и при этом никаких изменений в окружающих телах не происходило бы).

Крутим себе заряд по этой траектории, черпаем неограниченное количество энергии ниоткуда — и все энергетические проблемы человечества решены 🙂  Но такого, увы, не наблюдается — это вопиющим образом противоречит закону сохранения энергии. Так как электростатическое поле потенциально, мы можем говорить о потенциальной энергии заряда в этом поле. Начнём с простого и важного случая.

 1.6 Потенциальная энергия заряда в однородном поле

Потенциальная энергия тела, поднятого над землёй, равна mgh. Случай заряда в однородном поле оказывается очень похожим на эту механическую ситуацию.

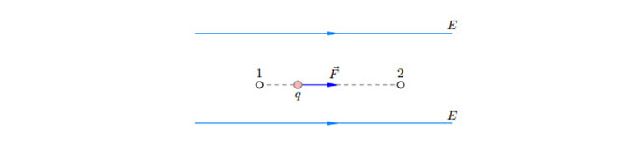
Рассмотрим однородное электростатическое поле E, линии напряжённости которого направлены вдоль оси X (рис. 8). Пусть положительный заряд q перемещается вдоль силовой линии из точки 1 (с координатой x1) в точку 2 (с координатой x2).

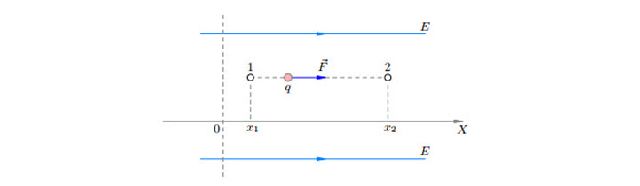 Рис. 8 Перемещение заряда в однородном поле

Поле действует на заряд с силой F, которая направлена вдоль линий напряжённости. Работа этой силы, как легко видеть, будет равна:

A = F(x2 − x1) = qE(x2 − x1).

Что изменится, если точки 1 и 2 не лежат на одной линии напряжённости? Оказывается, ничего! Формула для работы поля останется той же самой. Убедимся в этом с помощью рис. 9.

Рис. 9 Перемещение заряда в однородном поле

Двигаясь из точки 1 в точку 2, давайте выберем путь 1 → 3 → 2, где точка 3 лежит на одной силовой линии с точкой 1. Тогда работа A₃₂ на участке 32 равна нулю — ведь мы перемещаемся перпендикулярно силе. В результате получим:

A = A₁₃ + A₃₂ = A₁₃ = qE(x2 − x1).

Мы видим, что работа поля зависит лишь от абсцисс начального и конечного положений заряда.

Запишем полученную формулу следующим образом:

A = qEx2 − qEx1 = −((−qEx2) − (−qEx1)) = −(W2 − W1) = −∆W. (6)

Здесь W1 = −qEx1, W2 = −qEx2. Работа поля, в соответствии с формулой (6), оказывается равна изменению со знаком минус величины

W = −qEx.                            (7)

Эта величина и есть потенциальная энергия заряда в однородном электростатическом поле. Через x обозначена абсцисса точки, в которой ищется потенциальная энергия. Нулевой уровень потенциальной энергии в данном случае соответствует началу координат x = 0 и на рисунках изображён пунктирной линией, перпендикулярной линиям напряжённости.

Напомним, что пока считается q > 0. Из формулы (9) следует, что при движении заряда вдоль силовой линии потенциальная энергия убывает с ростом x. Это естественно: ведь поле совершает положительную работу, разгоняя заряд, а кинетическая энергия заряда растёт за счёт убыли его потенциальной энергии.

Несложно показать, что формула (9) остаётся справедливой и для q < 0. В этом случае потенциальная энергия возрастает с ростом x. Это тоже понятно: ведь сила, с которой поле действует на заряд, теперь будет направлена влево, так что движение заряда вправо будет осуществляться против действия поля. Заряд тормозится полем, кинетическая энергия заряда уменьшается, а потенциальная энергия — увеличивается.

Итак, важный вывод: в формуле для потенциальной энергии через q обозначается алгебраическая величина заряда (с учётом знака), а не его модуль.

1.7 Потенциал

Из формулы W = −qEx мы видим, что потенциальная энергия заряда q в однородном поле прямо пропорциональна этому заряду.

То же самое мы видим из формулы W = kq₁q₂/r: потенциальная энергия заряда q₁, находящегося в поле точечного заряда q₂, прямо пропорциональна величине заряда q₁.

Оказывается, это общий факт: потенциальная энергия W заряда q в любом электростатическом поле прямо пропорциональна величине q:

W = qϕ                  (8)

Величина ϕ уже не зависит от заряда, является характеристикой поля и называется потенциалом:

ϕ = W q .             (9)

Так, потенциал однородного поля E в точке с абсциссой x равен:

ϕ = −Ex.              (10)

Напомним, что ось X совпадает с линией напряжённости поля. Мы видим, что с ростом координаты x потенциал убывает. Иными словами, вектор напряжённости поля указывает направление убывания потенциала.

Для потенциала поля точечного заряда q на расстоянии r от него имеем:

ϕ = kq/r .               (11)

Единицей измерения потенциала служит хорошо известный вам вольт. Из формулы (9) мы видим, что В = Дж/Кл.

Итак, теперь у нас есть две характеристики поля: силовая (напряжённость) и энергетическая (потенциал). У каждой из них имеются свои преимущества и недостатки. Какую именно характеристику удобнее использовать — зависит от конкретной задачи.

 1.8 Разность потенциалов

Пусть заряд q перемещается в электростатическом поле из точки 1 в точку 2. Траектория заряда, напомним, роли не играет — работа поля A от этой траектории не зависит и равна разности потенциальных энергий заряда в начальной и конечной точках:

A = −∆W = −(W2 − W1) = W1 − W2.

С учётом формулы (11) имеем:

A = qϕ1 − qϕ2 = q(ϕ1 − ϕ2).                          (12)

Здесь ϕ1 — потенциал поля в точке 1, ϕ2 — потенциал поля в точке 2. Величина ϕ1 − ϕ2, от которой зависит работа поля, так и называется: разность потенциалов. Обратите внимание, что разность потенциалов есть потенциал начальной точки минус потенциал конечной точки, а не наоборот!

Разность потенциалов называется также напряжением между точками 1 и 2 и обозначается через U:

U = ϕ1 − ϕ2.                        (13)

Наряду с формулой (13) получаем тогда:

A = qU.                                (14)

Записывая формулы (12) и (14) в виде:

U = ϕ1 − ϕ2 = A q ,             (15)

получаем полезное истолкование напряжения: напряжение (или разность потенциалов) между данными точками — это работа поля по перемещению заряда из начальной точки в конечную, делённая на величину этого заряда.

Как и потенциальная энергия, потенциал определён с точностью до прибавления произвольной постоянной C: в зависимости от выбора точки, в которой потенциал полагается равным нулю, эта постоянная примет то или иное значение. Но физическим смыслом обладает не потенциал сам по себе, а напряжение (разность потенциалов). При вычитании потенциалов константа C сократится, и напряжение будет уже однозначно определённой величиной, не зависящей от выбора начала отсчёта потенциала.

Выбор точки нулевого потенциала позволяет истолковать в терминах работы сам потенциал. Действительно, пусть 1 — данная точка, 2 — точка нулевого потенциала. Тогда в формуле (15) имеем: ϕ1 = ϕ (потенциал в данной точке), ϕ2 = 0, A = A0 — работа поля по перемещению заряда q из данной точки в точку с нулевым потенциалом. В результате:

ϕ = A0 q .                     (16)

Таким образом, потенциал поля в данной точке — это работа поля по перемещению заряда из данной точки в точку нулевого потенциала, делённая на величину этого заряда.

1.9 Принцип суперпозиции для потенциалов

Рассмотрим электрическое поле, создаваемое системой из n заряженных тел. Это поле можно рассматривать как наложение полей, создаваемых каждым телом в отдельности.

Принцип суперпозиции для потенциалов. Пусть ϕ — потенциал результирующего поля в данной точке, а ϕ1, ϕ2, . . . , ϕn — потенциалы полей каждого из тел. Тогда:

                                 ϕ = ϕ1 + ϕ2 + . . . + ϕn.                        (17)

Иными словами, потенциал результирующего поля равен алгебраической сумме потенциалов полей, создаваемых каждым из тел в отдельности. Принцип суперпозиции для потенциалов вытекает из формулы (16) и из того факта, что работа равнодействующей силы есть сумма работ её слагаемых.

1.10  Однородное поле: связь напряжения и напряжённости

Предположим, что положительный заряд q перемещается в однородном электростатическом поле по направлению силовой линии из точки 1 в точку 2 (рис. 10). Расстояние между точками равно d.

Рис. 10  К выводу формулы U = Ed

C одной стороны, работа поля равна произведению силы на путь:

A = F d = qEd.

Работа получается положительной, так как сила и перемещение со направлены.

C другой стороны, работа поля есть произведение заряда на разность потенциалов между точками 1 и 2:

A = qU.

(Напряжение также положительно, так как ϕ1 > ϕ2 — ведь напряжённость направлена в сторону убывания потенциала.) Приравнивая правые части последних двух формул, получим: qU = qEd, откуда

U = Ed.                   (18)

Эта простая формула позволяет находить напряжение между точками однородного поля E, находящимися на одной силовой линии; при этом напряжённость поля направлена от начальной точки к конечной.

Выразим из формулы (21) напряжённость:

E = U/d .                  (19)

Эта формула пригодится нам впоследствии, при нахождении напряжённости поля в конденсаторе. А сейчас обратим внимание на одно следствие данной формулы: единицей измерения напряжённости является В/м. Эта единица используется чаще, чем первоначальная Н/Кл. Что ж, немало вещей пришлось узнать, чтобы понять равенство Н/Кл = В/м.