Законы Кирхгофа – первый и второй
Лекция № 18 Последовательное и параллельное соединение проводников. Правила Кирхгофа.
1 Соединения проводников
Есть два основных способа соединения проводников друг с другом — это последовательное и параллельное соединения. Различные комбинации последовательного и параллельного соединений приводят к смешанному соединению проводников. Мы будем изучать свойства этих соединений, но сначала нам понадобится некоторая вводная информация.
1.1 Резисторы и подводящие провода
Проводник, обладающий сопротивлением R, мы называем резистором и изображаем следующим образом (рис. 1):
Рис. 1 Резистор
Напряжение на резисторе — это разность потенциалов стационарного электрического поля между концами резистора. Между какими именно концами? В общем-то, это неважно, но обычно удобно согласовывать разность потенциалов с направлением тока.
Ток в цепи течёт от «плюса» источника к «минусу». В этом направлении потенциал стационарного поля убывает. Напомним ещё раз, почему это так.
Пусть положительный заряд q перемещается по цепи из точки a в точку b, проходя через резистор R (рис. 2):
Рис.2 U = φa – φb
Стационарное поле совершает при этом положительную работу A = q(φa − φb). Так как q > 0 и A > 0, то и φa − φb > 0, т. е. φa > φb.
Поэтому напряжение на резисторе мы вычисляем как разность потенциалов в направлении тока: U = φa − φb.
Сопротивление подводящих проводов обычно пренебрежимо мало; на электрических схемах оно считается равным нулю. Из закона Ома следует тогда, что потенциал не меняется вдоль провода: ведь если φa − φb = IR и R = 0, то φa = φb (рис. 3):
Рис.3 φa = φb
Таким образом, при рассмотрении электрических цепей мы пользуемся идеализацией, которая сильно упрощает их изучение. А именно, мы считаем, что потенциал стационарного поля изменяется лишь при переходе через отдельные элементы цепи, а вдоль каждого соединительного провода остаётся неизменным. В реальных цепях потенциал монотонно убывает при движении от положительной клеммы источника к отрицательной.
1.2 Последовательное соединение
При последовательном соединении проводников конец каждого проводника соединяется с началом следующего за ним проводника.
Рассмотрим два резистора R1 и R2, соединённых последовательно и подключённых к источнику постоянного напряжения U (рис. 4). Напомним, что положительная клемма источника обозначается более длинной чертой, так что ток в данной схеме течёт по часовой стрелке.
Рис.4 Последовательное соединение
Сформулируем основные свойства последовательного соединения и проиллюстрируем их на этом простом примере:
- При последовательном соединении проводников сила тока в них одинакова. В самом деле, через любое поперечное сечение любого проводника за одну секунду будет проходить один и тот же заряд. Ведь заряды нигде не накапливаются, из цепи наружу не уходят и не поступают в цепь извне.
- Напряжение на участке, состоящем из последовательно соединённых проводников, равно сумме напряжений на каждом проводнике. Действительно, напряжение Uab на участке ab — это работа поля по переносу единичного заряда из точки a в точку b; напряжение Ubc на участке bc — это работа поля по переносу единичного заряда из точки b в точку c. Складываясь, эти две работы дадут работу поля по переносу единичного заряда из точки a в точку c, то есть напряжение U на всём участке: U = Uab + Ubc.
Можно и более формально, без всяких словесных объяснений: U = Uac = φa − φc = (φa − φb) + (φb − φc) = Uab + Ubc.
- Сопротивление участка, состоящего из последовательно соединённых проводников, равно сумме сопротивлений каждого проводника. Пусть R — сопротивление участка ac. По закону Ома имеем:
что и требовалось.
Можно дать интуитивно понятное объяснение правила сложения сопротивлений на одном частном примере. Пусть последовательно соединены два проводника из одинакового вещества и с одинаковой площадью поперечного сечения S, но с разными длинами l1 и l2.
Сопротивления проводников равны:
Но это, повторяем, лишь частный пример. Сопротивления будут складываться и в самом общем случае — если различны также вещества проводников и их поперечные сечения. Доказательство этого даётся с помощью закона Ома, как показано выше. Наши доказательства свойств последовательного соединения, приведённые для двух проводников, переносятся без существенных изменений на случай произвольного числа проводников.
1.3 Параллельное соединение
При параллельном соединении проводников их начала подсоединяются к одной точке цепи, а концы — к другой точке.
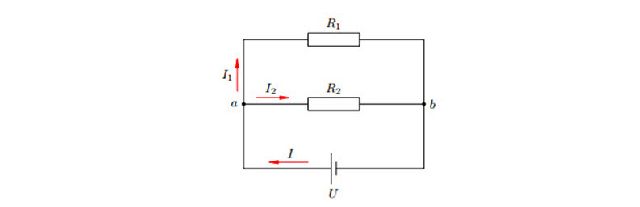
Снова рассматриваем два резистора, на сей раз соединённые параллельно (рис. 5).
Рис.5 Параллельное соединение
Резисторы подсоединены к двум точкам: a и b. Эти точки называются узлами или точками разветвления цепи. Параллельные участки называются также ветвями; участок от b к a (по направлению тока) называется неразветвленной частью цепи.
Теперь сформулируем свойства параллельного соединения и докажем их для изображённого выше случая двух резисторов:
- Напряжение на каждой ветви одинаково и равно напряжению на неразветвленной части цепи. В самом деле, оба напряжения U1 и U2 на резисторах R1 и R2 равны разности потенциалов между точками подключения:
U1 = U2 = φa − φb = U.
Этот факт служит наиболее отчётливым проявлением потенциальности стационарного электрического поля движущихся зарядов.
- Сила тока в неразветвленной части цепи равна сумме сил токов в каждой ветви. Пусть, например, в точку a за время t из неразветвленного участка поступает заряд q. За это же время t из точки a к резистору R1 уходит заряд q1, а к резистору R2 — заряд q2. Ясно, что q = q1 + q2. В противном случае в точке a накапливался бы заряд, меняя потенциал данной точки, что невозможно (ведь ток постоянный, поле движущихся зарядов стационарно, и потенциал каждой точки цепи не меняется со временем). Тогда имеем:
что и требовалось.
- Величина, обратная сопротивлению участка параллельного соединения, равна сумме величин, обратных сопротивлениям ветвей. Пусть R — сопротивление разветвлённого участка ab. Напряжение на участке ab равно U; ток, текущий через этот участок, равен I. Поэтому:
Сокращая на U, получим:
1/R = 1/R1 + 1/R2 , (1)
что и требовалось.
Как и в случае последовательного соединения, можно дать объяснение данного правила на частном примере, не обращаясь к закону Ома.
Пусть параллельно соединены проводники из одного вещества с одинаковыми длинами l, но разными поперечными сечениями S1 и S2. Тогда это соединение можно рассматривать как проводник той же длины l, но с площадью сечения S = S1 + S2. Имеем:
Приведённые доказательства свойств параллельного соединения без существенных изменений переносятся на случай любого числа проводников.
Из соотношения (1) можно найти R:
R = R1R2/(R1 + R2) . (2)
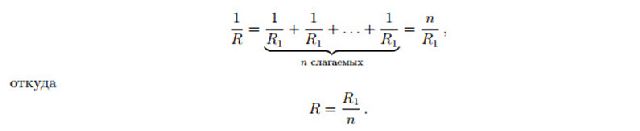
К сожалению, в общем случае n параллельно соединённых проводников компактного аналога формулы (2) не получается, и приходится довольствоваться соотношением
1/R = 1/R1 + 1/R2 + . . . + 1/Rn . (3)
Тем не менее, один полезный вывод из формулы (3) сделать можно. Именно, пусть сопротивления всех n резисторов одинаковы и равны R1. Тогда:
Мы видим, что сопротивление участка из n параллельно соединённых одинаковых проводников в n раз меньше сопротивления одного проводника.
1.4 Смешанное соединение
Смешанное соединение проводников, как следует из названия, может являться совокупностью любых комбинаций последовательного и параллельного соединений, причём в состав этих соединений могут входить как отдельные резисторы, так и более сложные составные участки.
Расчёт смешанного соединения опирается на уже известные свойства последовательного и параллельного соединений. Ничего нового тут уже нет: нужно только аккуратно расчленить данную схему на более простые участки, соединённые последовательно или параллельно.
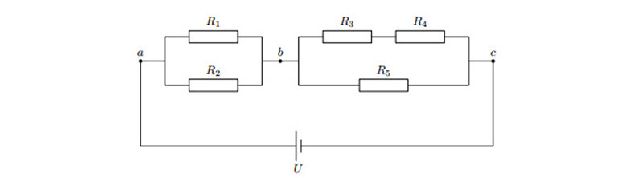
Рассмотрим пример смешанного соединения проводников (рис. 6).
Рис. 6 Смешанное соединение
Пусть U = 14 В, R1 = 2 Ом, R2 = 3 Ом, R3 = 3 Ом, R4 = 5 Ом, R5 = 2 Ом. Найдём силу тока в цепи и в каждом из резисторов.
Наша цепь состоит из двух последовательно соединённых участков ab и bc. Сопротивление участка ab:
Сопротивление цепи: R = Rab + Rbc = 1,2 + 1,6 = 2,8 Ом.
Теперь находим силу тока в цепи:
I = U/R = 14/2,8 = 5 A.
Для нахождения тока в каждом резисторе вычислим напряжения на обоих участках:
Uab = IRab = 5 · 1,2 = 6 B;
Ubc = IRbc = 5 · 1,6 = 8 B.
(Заметим попутно, что сумма этих напряжений равна 14 В, т. е. напряжению в цепи, как и должно быть при последовательном соединении.)
Оба резистора R1 и R2 находятся под напряжением Uab, поэтому:
Стало быть, через резистор R5 течёт ток I5 = I − I3 = 5 − 1 = 4 A
Законы Кирхгофа
Законы Кирхгофа – правила, которые показывают, как соотносятся токи и напряжения в электрических цепях. Эти правила были сформулированы Густавом Кирхгофом в 1845 году. В литературе часто называют законами Кирхгофа, но это не верно, так как они не являются законами природы, а были выведены из третьего уравнения Максвелла при неизменном магнитном поле. Но все же, первое более привычное для них название, поэтому и мы будет их называть, как это принято в литературе – законы Кирхгофа.
Первый закон Кирхгофа – сумма токов сходящихся в узле равна нулю.
Давайте разбираться. Узел это точка, соединяющая ветви. Ветвью называется участок цепи между узлами. На рисунке видно, что ток i входит в узел, а из узла выходят токи i1 и i2. Составляем выражение по первому закона Кирхгофа, учитывая, что токи, входящие в узел имеют знак плюс, а токи, исходящие из узла имеют знак минус i-i1-i2=0. Ток i как бы растекается на два тока поменьше и равен сумме токов i1 и i2 i=i1+i2. Но если бы, например, ток i2 входил в узел, тогда бы ток I определялся как i=i1-i2. Важно учитывать знаки при составлении уравнения.
Первый закон Кирхгофа это следствие закона сохранения электричества: заряд, приходящий к узлу за некоторый промежуток времени, равен заряду, уходящему за этот же интервал времени от узла, т.е. электрический заряд в узле не накапливается и не исчезает.
Второй закон Кирхгофа – алгебраическая сумма ЭДС, действующая в замкнутом контуре, равна алгебраической сумме падений напряжения в этом контуре.
Напряжение выражено как произведение тока на сопротивление (по закону Ома).
В этом законе тоже существуют свои правила по применению. Для начала нужно задать стрелкой направление обхода контура. Затем просуммировать ЭДС и напряжения соответственно, беря со знаком плюс, если величина совпадает с направлением обхода и минус, если не совпадает. Составим уравнение по второму закону Кирхгофа, для нашей схемы. Смотрим на нашу стрелку, E2 и Е3 совпадают с ней по направлению, значит знак плюс, а Е1 направлено в противоположную сторону, значит знак минус. Теперь смотрим на напряжения, ток I1 совпадает по направлению со стрелкой, а токи I2 и I3 направлены противоположно. Следовательно:
— E1 + E2 + E3 = I1R1 — I2R2 — I3R3
На основании законов Кирхгофа составлены методы анализа цепей переменного синусоидального тока. Метод контурных токов – метод, основанный на применении второго закона Кирхгофа и метод узловых потенциалов основанный на применении первого закона Кирхгофа.





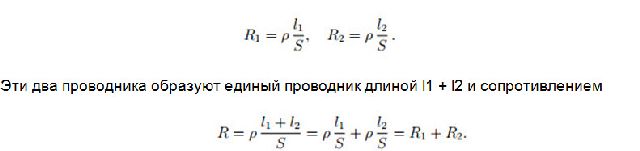
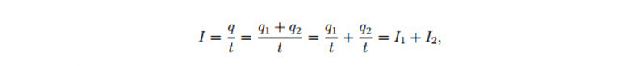
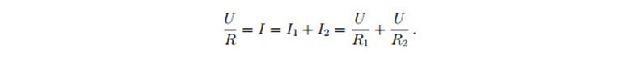


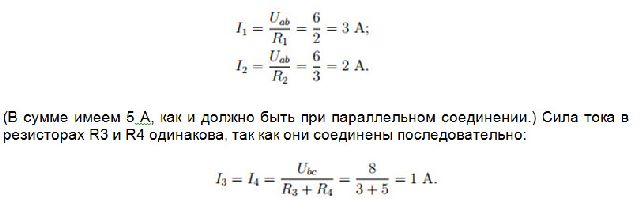

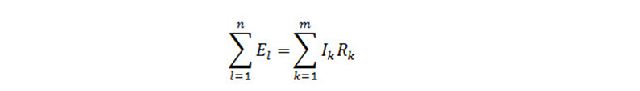

![Синдикация через RSS [x]](http://razmishlyajem.ru/wp-content/themes/mad-meg/images/rss.png)
Всё хорошо, только не законы, а правила Кирхгофа… Перед написанием статьи надо бы разобраться, что такое закон, а что такое правило.
Еще бы хорошо, было бы тогда, когда это писал человек знающий!
Иногда законы Кирхгофа называют правилами Кирхгофа, особенно в старой литературе.
Итак, для начала напомню все-таки суть первого и второго закона Кирхгофа, а далее рассмотрим примеры расчета токов, напряжений в электрических цепях, с практическими примерами и ответами на вопросы, которые задавались мне в комментариях на сайте.
Это я привел пример с учебного сайта.
Так что можно сказать, что вы просто устарели, да и логин у вас подходит к этому!