Взаимодействие тел, законы динамики Ньютона  

Лекция № 4 Взаимодействие тел. Принцип суперпозиции сил. Законы динамики Ньютона. Силы в природе.

Законы Кеплера, закон всемирного тяготения

Еще в глубокой древности было замечено, что в отличие от звезд, которые неизменно сохраняют свое взаимное расположение в пространстве в течение столетий, планеты описывают среди звезд сложнейшие траектории. Для объяснения петлеобразного дви­жения планет древнегреческий ученый К. Птоломей (II в. н. э.), считая Землю рас­положенной в центре Вселенной, предположил, что каждая из планет движется по малому кругу (эпициклу), центр которого равномерно движется по большому кругу, в центре которого находится Земля. Эта концепция получила название птоломеевой геоцентрической системы мира.

В начале XVI в. польским астрономом Н. Коперником (1473—1543) обоснована гелиоцентрическая система, согласно которой движения небесных тел объясняются движением Земли (а также других планет) вокруг Солнца и суточным вращением Земли. Теория и наблюдения Коперника воспринимались как занимательная фантазия.

К началу XVII столетия большинство ученых убедилось, однако, в справедливости гелиоцентрической системы мира. И. Кеплер (1571—1630), обработав и уточнив ре­зультаты многочисленных наблюдений датского астронома Т. Браге (1546—1601), изложил законы движения планет:

1.Каждая планета движется по эллипсу, в одном из фокусов которого находится Солнце.

2.Радиус-вектор планеты за равные промежутки времени описывает одинаковые площади.

3.Квадраты периодов обращения планет вокруг Солнца относятся как кубы больших полуосей их орбит.

Впоследствии И. Ньютон, изучая движение небесных тел, на основании законов Кеплера и основных законов динамики открыл всеобщий закон всемирного тяготения: между любыми двумя материальными точками действует сила взаимного притяжения, прямо пропорциональная произведению масс этих точек (m₁ и т₂) и обратно пропорци­ональная квадрату расстояния между ними (r²):

F= G (m1*m2/r^2)                                                                      (1)

Эта сила называется гравитационной (или силой всемирного тяготения). Силы тяготения всегда являются силами притяжения и направлены вдоль прямой, проходящей через взаимодействующие тела. Коэффициент пропорциональности G называется гравитаци­онной постоянной.

Закон всемирного тяготения установлен для тел, принимаемых за материальные точки, т. е. для таких тел, размеры которых малы по сравнению с расстоянием между ними. Если же размеры взаимодействующих тел сравнимы с расстоянием между ними, то эти тела надо разбить на точечные элементы, подсчитать по формуле (1) силы притяжения между всеми попарно взятыми элементами, а затем геометрически их сложить (проинтегрировать), что является довольно сложной математической задачей.

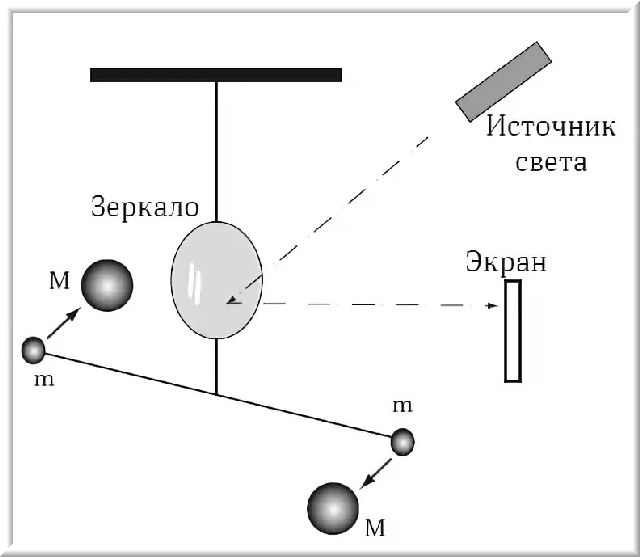
Впервые экспериментальное доказательство закона всемирного тяготения для земных тел, а также числовое определение гравитационной постоянной G проведено английским физиком Г. Кавендишем (1731—1810). Принципиальная схема опыта Кавендиша, применившего крутильные весы, представлена на рис.1. Легкое коромысло А с двумя одинаковыми шариками массой m=729 г подвешено на упругой нити В. На коромысле С укреплены на той же высоте массивные шары массой M=158 кг. Поворачивая коромысло С вокруг вертикальной оси, можно изменять расстояние между шарами с массами т и М. Под действием пары сил, приложенных к шарам т со стороны шаров М, коромысло А поворачивается в горизонтальной плоскости, закручи­вая нить В до тех пор, пока момент сил упругости не уравновесит момента сил тяготения. Зная упругие свойства нити, по измеренному углу поворота можно найти возникающие силы притяжения, а так как массы шаров известны, то и вычислить значение G.

Рис.1 Крутильные весы Г.Кавендиша

Значение G, приводимое в таблицах фундаментальных физических постоянных, принимается равным 6,6720*10^–11 Н*м/кг², т. е. два точечных тела массой по 1 кг каждое, находящиеся на расстоянии 1 м друг от друга, притягиваются с силой 6,6720*10^–11 H. Очень малая величина G показывает, что сила гравитационного взаимодействия может быть значительной только в случае больших масс.

Законы динамики Ньютона

Первый закон Ньютона, масса и сила

Динамика является основным разделом механики, в ее основе лежат три закона Ньютона, сформулированные им в 1687 г. Законы Ньютона играют исключительную роль в механике и являются (как и все физические законы) обобщением результатов огромного человеческого опыта. Их рассматривают как систему взаимосвязанных законов и опытной проверке подвергают не каждый отдельный закон, а всю систему в целом.

Первый закон Ньютона: всякая материальная точка (тело) сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока воздействие со стороны других тел не заставит ее изменить это состояние. Стремление тела сохранять состояние покоя или равномерного прямолинейного движения называется инертностью. Поэтому первый закон Ньютона называют также законом инерции.

Механическое движение относительно, и его характер зависит от системы отсчета. Первый закон Ньютона выполняется не во всякой системе отсчета, а те системы, по отношению к которым он выполняется, называются инерциальными системами отсчета. Инерциальной системой отсчета является такая система отсчета, относительно которой материальная точка, свободная от внешних воздействий, либо покоится, либо движется равномерно и прямолинейно. Первый закон Ньютона утверждает существование инерциальных систем отсчета.

Опытным путем установлено, что инерциальной можно считать гелиоцентрическую (звездную) систему отсчета (начало координат находится в центре Солнца, а оси проведаны в направлении определенных звезд). Система отсчета, связанная с Землей, строго говоря, неинерциальная, однако эффекты, обусловленные ее неинерциальностью (Земля вращается вокруг собственной оси и вокруг Солнца), при решении многих задач пренебрежимо малы, и в этих случаях ее можно считать инерциальной.

Из опыта известно, что при одинаковых воздействиях различные тела неодинаково изменяют скорость своего движения, т.е., иными словами, приобретают различные ускорения. Ускорение зависит не только от величины воздействия, но и от свойств самого тела (от его массы).

Масса тела — физическая величина, являющаяся одной из основных характеристик материи, определяющая ее инерционные (инертная масса) и гравитационные (гравитационная масса) свойства. В настоящее время можно считать доказанным, что инертная и гравитационная массы равны друг другу (с точностью, не меньшей 10–12 их значения).

Чтобы описывать воздействия, упоминаемые в первом законе Ньютона, вводят понятие силы. Под действием сил тела либо изменяют скорость движения, т. е. приобретают ускорения (динамическое проявление сил), либо деформируются, т. е. изменяют свою форму и размеры (статическое проявление сил). В каждый момент времени сила характеризуется числовым значением, направлением в пространстве и точкой приложения. Итак, сила — это векторная величина, являющаяся мерой механического воздействия на тело со стороны других тел или полей, в результате, которого тело приобретает ускорение или изменяет свою форму и размеры.

Силы в механике

Все многообразие встречающихся в природе взаимодействий сводится всего лишь к четырем типам. Это гравитационное электромагнитное, ядерное (или сильное) и слабое взаимодействие. В механике Ньютона  можно рассматривать только гравитационное и электромагнитное взаимодействия.

Ядерное и слабое взаимодействие действует на небольших расстояниях. Гравитационное и электромагнитное взаимодействие отличаются дальнодействием: их действие проявляются на очень больших расстояниях.

Название силы	Природа взаимодействия	Формула для расчета силы	Зависимость силы от расстояния или относительной скорости	Зависит ли сила от массы взаимодействующих тел	Как направлена сила
Сила тяготе-ния	гравитационная	F=G(m1*m2)/R^2	Является функцией расстояния между взаимодействующими телами	Прямо пропорциональ-на массам взаимодействующих тел	Вдоль прямой, соединяющей взаимодействующие тела
Сила упру-гости	электромагнитная	F= -k*r	Является функцией расстояния (зависит от деформации)	Не зависит	Противоположно направлению перемещения частиц при деформации
Сила тренияа) су-хогоб) жид-кого	электромагнитная	Fтр=f*N	Является функцией скорости относительного движения	Не зависит	Противоположно направлению вектора скорости

В таблице применены следующие обозначения:

• k – упругость;
• r – радиус вектор;
• f – коэффициент трения скольжения;
• N – сила нормального давления.

Второй закон Ньютона

Второй закон Ньютона — основной закон динамики поступательного движения — отвечает на вопрос, как изменяется механическое движение материальной точки (тела) под действием приложенных к ней сил.

Если рассмотреть действие различных сил на одно и то же тело, то оказывается, что ускорение, приобретаемое телом, всегда прямо пропорционально равнодействующей приложенных сил:

а ~ F (m = const).                                                   (1)

При действии одной и той же силы на тела с разными массами их ускорения оказываются различными, а именно

а ~ 1/m (F = const).                                                (2)

Используя выражения (1) и (2) и учитывая, что сила и ускорение — величины векторные, можем записать

а = kF/m.                                                                  (3)

Соотношение (6.3) выражает второй закон Ньютона: ускорение, приобретаемое материальной точкой (телом), пропорционально вызывающей его силе, совпадает с нею по направлению и обратно пропорционально массе материальной точки (тела).

В СИ коэффициент пропорциональности k= 1. Тогда

a = F/m

или

F = m*a = m*(dv/dt)                                                   (4)

Учитывая, что масса материальной точки (тела) в классической механике есть величина постоянная, в выражении (4) ее можно внести под знак производной:

F =  (d/dt)(m*v)                                                            (5)

Векторная величина

P = m*v                                                                            (6)

численно равная произведению массы материальной точки на ее скорость и имеющая направление скорости, называется импульсом (количеством движения) этой материальной точки.

Подставляя (6) в (5), получим

F =  dp/dt                                                                          (7)

Это выражение — более общая формулировка второго закона Ньютона: скорость изменения импульса материальной точки равна действующей на нее силе. Выражение (7) называется уравнением движения материальной точки.

Единица силы в СИ — ньютон (Н): 1 Н — сила, которая массе 1 кг сообщает ускорение 1 м/с² в направлении действия силы:

1 Н = 1 кг*м/с².

Второй закон Ньютона справедлив только в инерциальных системах отсчета. Первый закон Ньютона можно получить из второго. Действительно, в случае равенства нулю равнодействующей сил (при отсутствии воздействия на тело со стороны других тел) ускорение (см. (3)) также равно нулю. Однако первый закон Ньютона рассматривается как самостоятельный закон (а не как следствие второго закона), так как именно он утверждает существование инерциальных систем отсчета, в которых только и выполняется уравнение (7).

В механике большое значение имеет принцип независимости действия сил: если на материальную точку действует одновременно несколько сил, то каждая из этих сил сообщает материальной точке ускорение согласно второму закону Ньютона, как будто других сил не было. Согласно этому принципу, силы и ускорения можно разлагать на составляющие, использование которых приводит к существенному упрощению решения задач. Например, на рис. 2 действующая сила F=ma разложена на два компонента: тангенциальную силу Fτ, (направлена по касательной к траектории) и нормальную силу Fn (направлена по нормали к центру кривизны).

Рис.2 Принцип независимости действия сил (принцип суперпозиции)

Если на материальную точку действует одновременно несколько сил, то, согласно принципу независимости действия сил, под F во втором законе Ньютона понимают результирующую силу.

Третий закон Ньютона

Взаимодействие между материальными точками (телами) определяется третьим законом Ньютона: всякое действие материальных точек (тел) друг на друга носит характер взаимодействия; силы, с которыми действуют друг на друга материальные точки, всегда равны по модулю, противоположно направлены и действуют вдоль прямой, соединяющей эти точки:

F12 = – F21,                                                                          (7)

где F12 — сила, действующая на первую материальную точку со стороны второй;

F21 — сила, действующая на вторую материальную точку со стороны первой. Эти силы приложены к разным материальным точкам (телам), всегда действуют парами и являются силами одной природы.

Третий закон Ньютона позволяет осуществить переход от динамики отдельной материальной точки к динамике системы материальных точек. Это следует из того, что и для системы материальных точек взаимодействие сводится к силам парного взаимодействия между материальными точками.

Сила тяжести и вес, невесомость

На любое тело, расположенное вблизи поверхности Земли, действует сила тяготения F, под влиянием которой и в согласии со вторым законом Ньютона тело начнет двигаться с ускорением свободного падения g. Таким образом, в системе отсчета, связанной с Землей, на всякое тело массой т действует сила

P = m*g

называемая  силой тяжести.

Согласно фундаментальному физическому закону — обобщенному закону Галилея, все тела в одном и том же поле тяготения падают с одинаковым ускорением. Следовательно, в данном месте Земли ускорение свободного падения одинаково для всех тел. Оно изменяется вблизи поверхности Земли с широтой в пределах от 9,780 м/с² на экваторе до 9,832 м/с² на полюсах. Это обусловлено суточным вращением Земли вокруг своей оси, с одной стороны, и сплюснутостью Земли — с другой (экваториальный и полярный радиусы Земли равны соответственно 6378 и 6357 км). Так как различие значений g невелико, ускорение свободного падения, которое используется при решении практических задач, принимается равным 9,81 м/с².

Если пренебречь суточным вращением Земли вокруг своей оси, то сила тяжести и сила гравитационного тяготения равны между собой:

P = m*g = F =G*m*M/R²

где М — масса Земли; R — расстояние между телом и центром Земли. Эта формула дана для случая, когда тело находится на поверхности Земли.

Пусть тело расположено на высоте h от поверхности Земли, R₀ — радиус Земли, тогда

P = G*m*M/(R0+h)^2

т. е. сила тяжести с удалением от поверхности Земли уменьшается.

В физике применяется также понятие веса тела. Весом тела называют силу, с кото­рой тело вследствие тяготения к Земле действует на опору (или подвес), удерживающую тело от свободного падения. Вес тела проявляется только в том случае, если тело движется с ускорением, отличным от g, т. е. когда на тело кроме силы тяжести действуют другие силы. Состояние тела, при котором оно движется только под действием силы тяжести, называется состоянием невесомости.

Таким образом, сила тяжести действует всегда, а вес проявляется только в том случае, когда на тело кроме силы тяжести действуют еще другие силы, вследствие чего тело движется с ускорением а, отличным от g. Если тело движется в поле тяготения Земли с ускорением a≠ g, то к этому телу приложена дополнительная сила N, удовлет­воряющая условию

N + P = m*a

Тогда вес тела

P’ = -N = P — ma = mg — ma =  m(g-a)

т. е. если тело покоится или движется прямолинейно и равномерно, то а=0 и P‘=mg. Если тело свободно движется в поле тяготения по любой траектории и в любом направлении, то a=g и Р’=0, т. е. тело будет невесомым. Например, невесомыми являются тела, находящиеся в космических кораблях, свободно движущихся в космосе.

Закон сохранения импульса

В классической механике существуют два закона сохранения: закон сохранения импульса и закон сохранения энергии.

 Импульс тела

Впервые понятие импульса ввёл французский математик, физик, механик и философ Декарт, назвавший импульс количеством движения.

С латинского «импульс» переводится как «толкать, двигать».

Любое тело, которое движется, обладает импульсом.

Представим себе тележку, стоящую неподвижно. Её импульс равен нулю. Но как только тележка начнёт двигаться, её импульс перестанет быть нулевым. Он начнёт изменяться, так как будет изменяться скорость.

Импульс материальной точки, или количество движения, – векторная величина, равная произведению массы точки на её скорость. Направление вектора импульса точки совпадает с направлением вектора скорости.

Р = m*v

Если говорят о твёрдом физическом теле, то импульсом такого тела называют произведение массы этого тела на скорость центра масс.

Как вычислить импульс тела? Можно представить, что тело состоит из множества материальных точек, или системы материальных точек.

Если  P_i = m_i*v_i  — импульс одной материальной точки, то импульс системы материальных точек

P = Σm_i*v_i

То есть, импульс системы материальных точек – это векторная сумма импульсов всех материальных точек, входящих в систему. Она равна произведению масс этих точек на их скорости.

Единица измерения импульса в международной системе единиц СИ – килограмм-метр в секунду (кг · м/сек).

Импульс силы

В механике существует тесная связь между импульсом тела и силой. Эти две величины связывает величина, которая называется импульсом силы.

Если на тело действует постоянная сила F в течение промежутка времени t, то согласно второму закону Ньютона

F = m*a = m(v – v₀)/t

F*t = m*v – m*v₀

Эта формула показывает связь между силой, которая действует на тело, временем действия этой силы и изменением скорости тела.

Величина, равная произведению силы, действующей на тело, на время, в течение которого она действует, называется импульсом силы.

Как мы видим из уравнения, импульс силы равен разности импульсов тела в начальный и конечный момент времени, или изменению импульса за какое-то время.

Второй закон Ньютона в импульсной форме формулируется следующим образом: изменение импульса тела равно импульсу действующей на него силы. Нужно сказать, что сам Ньютон именно так и сформулировал первоначально свой закон.

Импульс силы – это также векторная величина.

Закон сохранения импульса

Закон сохранения импульса вытекает из третьего закона Ньютона.

Нужно помнить, что этот закон действует только в замкнутой, или изолированной, физической системе. А замкнутой называют такую систему, в которой тела взаимодействуют только между собой и не взаимодействуют с внешними телами.

Представим замкнутую систему из двух физических тел. Силы взаимодействия тел друг с другом называют внутренними силами.

Импульс силы для первого тела равен

F*t = m_1*v’₁ – m₁*v₁

Согласно третьему закону Ньютона силы, которые действуют на тела при их взаимодействии, равны по величине и противоположны по направлению.

Следовательно, для второго тела импульс силы равен

F*t = m_2*v’₂ – m₂*v₂

Путём простых вычислений получаем математическое выражение закона сохранения импульса:

m₁*v₁ + m₂*v₂  = m_1*v’₁ + m_2*v’₂

где m₁ и m₂ – массы тел,

v₁ и v₂ – скорости первого и второго тел до взаимодействия,

v₁‘ и v₂‘ – скорости первого и второго тел после взаимодействия.

p₁ = m₁ · v₁    — импульс первого тела до взаимодействия;

p₂ = m₂ · v₂     — импульс второго тела до взаимодействия;

p ₁‘= m₁ · v₁‘  — импульс первого тела после взаимодействия;

p₂ ‘= m₂ · v₂‘  — импульс второго тела после взаимодействия;

То есть

p₁ + p₂ = p₁‘ + p₂‘

В замкнутой системе тела только обмениваются импульсами. А векторная сумма импульсов этих тел до их взаимодействия равна векторной сумме их импульсов после взаимодействия.

Так, в результате выстрела из ружья импульс самого ружья и импульс пули изменятся. Но сумма импульсов ружья и находящейся в нём пули до выстрела останется равной сумме импульсов ружья и летящей пули после выстрела.

При стрельбе из пушки возникает отдача. Снаряд летит вперёд, а само орудие откатывается назад. Снаряд и пушка – замкнутая система, в которой действует закон сохранения импульса.

Импульс каждого из тел в замкнутой системе может изменяться в результате их взаимодействия друг с другом. Но векторная сумма импульсов тел, входящих в замкнутую систему, не изменяется при взаимодействии этих тел с течением времени, то есть остаётся постоянной величиной. Это и есть закон сохранения импульса.

Более точно закон сохранения импульса формулируется следующим образом: векторная сумма импульсов всех тел замкнутой системы – величина постоянная, если внешние силы, действующие на неё, отсутствуют, или же их векторная сумма равна нулю.

Импульс системы тел может измениться только в результате действия на систему внешних сил. И тогда закон сохранения импульса действовать не будет.

Нужно сказать, что в природе замкнутых систем не существует. Но, если время действия внешних сил очень мало, например, во время взрыва, выстрела и т.п., то в этом случае воздействием внешних сил на систему пренебрегают, а саму систему рассматривают как замкнутую.

Кроме того, если на систему действуют внешние силы, но сумма их проекций на одну из координатных осей равна нулю, (то есть силы уравновешены в направлении этой оси), то в этом направлении закон сохранения импульса выполняется.

Закон сохранения импульса называют также законом сохранения количества движения.

Самый яркий пример применения закона сохранения импульса – реактивное движение.

Реактивное движение

Реактивным движением называют движение тела, которое возникает при отделении от него с определённой скоростью какой-то его части. Само тело получает при этом противоположно направленный импульс.

Самый простой пример реактивного движения – полёт воздушного шарика, из которого выходит воздух. Если мы надуем шарик и отпустим его, он начнёт лететь в сторону, противоположную движению выходящего из него воздуха.

Пример реактивного движения в природе – выброс жидкости из плода бешеного огурца, когда он лопается. При этом сам огурец летит в противоположную сторону.

Медузы, каракатицы и другие обитатели морских глубин передвигаются, вбирая воду, а затем выбрасывая её.

На законе сохранения импульса основана реактивная тяга. Мы знаем, что при движении ракеты с реактивным двигателем в результате сгорания топлива из сопла выбрасывается струя жидкости или газа (реактивная струя). В результате взаимодействия двигателя с вытекающим веществом появляется реактивная сила. Так как ракета вместе с выбрасываемым веществом является замкнутой системой, то импульс такой системы не меняется со временем.

Реактивная сила возникает в результате взаимодействия только частей системы. Внешние силы не оказывают никакого влияния на её появление.

До того, как ракета начала двигаться, сумма импульсов ракеты и горючего была равна нулю. Следовательно, по закону сохранения импульса после включения двигателей сумма этих импульсов тоже равна нулю.

m_r*Δv + Δm_f*u = 0

m_r*Δv  = — Δm_f*u

где  m_r — масса ракеты

u — скорость истечения газа

Δv — изменение скорости ракеты

∆m_f — расход массы топлива

Предположим, ракета работала в течение времени t.

Разделив обе части уравнения на ∆t, получим выражение

m_r*Δv/Δt = -(Δm_f*/Δt)*u

По второму закону Ньютона реактивная сила равна

F_r  = m_r*a = — u* Δm_f/Δt

Реактивная сила, или реактивная тяга, обеспечивает движение реактивного двигателя и объекта, связанного с ним, в сторону, противоположную направлению реактивной струи.

Реактивные двигатели применяются в современных самолётах и различных ракетах, военных, космических и других областях.